[edit]
1 왜도(skewness) #
왜도는 분포의 비대칭 정도를 측정하는 척도
skew.f<-function(x)
{
x<-as.matrix(x)
n<-nrow(x)
m<-cov.wt(x)$center
S<-cov.wt(x,method="ML")$cov
SI<-solve(S)
skew<-0
for(r in 1:n) {
for(s in 1:n) {
skew<-skew+(t(x[r,]-m)%*%SI%*%(x[s,]-m))^3
}
}
skew/(n^2)
}
[edit]
2 첨도(kurtosis) #
첨도는 분포의 윗 부분의 평평한 정도를 측정하는 척도
kurtosis.f<-function(x)
{
x<-as.matrix(x)
n<-nrow(x)
m<-cov.wt(x)$center
S<-cov.wt(x,method="ML")$cov
SI<-solve(S)
kurtosis<-0
for(r in 1:n) {
kurtosis<-kurtosis+( t(x[r,]-m) %*% SI %*% (x[r,]-m) )^2
}
kurtosis/n
}
[edit]
3 정규성 검정 #
normality.f<-function(x,alpha=0.05)
{
n<-nrow(x)
p<-ncol(x)
m<-(p*(p+1)*(p+2))/6
b1<-skew.f(x)
p.val<-1-pchisq((n*b1)/6,m)
cat("Skewness is ",b1,"and P-value is ",p.val,".\n")
if(p.val < alpha)
cat("Reject the normality.\n")
else
cat("Don't reject the normality.\n")
}
- alpah : 유의수준
- m: 자유도
- p.val: P-Value
다음과 같이 사용한다.
> source("normality.f")
> source("skew.f")
> source("kurtosis.f")
> cork.d <-read.table("cork.d", header=T)
> normality.f(cork.d)
Skewness is 4.476382 and P-value is 0.4036454 .
Don't reject the normality.
[edit]
4 카이제곱 그림 #
chiplot.f<-function(x)
{
n<-nrow(x)
p<-ncol(x)
mah<-sort(mahalanobis(x,mean(x),var(x)))
arr<-seq(from=1/(2*n),length=n,by=1/n);
chi.per<-qchisq(arr,p)
plot(mah,chi.per,xlab="Ordered Mahalanobis distance",ylab="Chi-sqare percentile");
}
> source("chiplot.f")
> chiplot.f(cork.d)
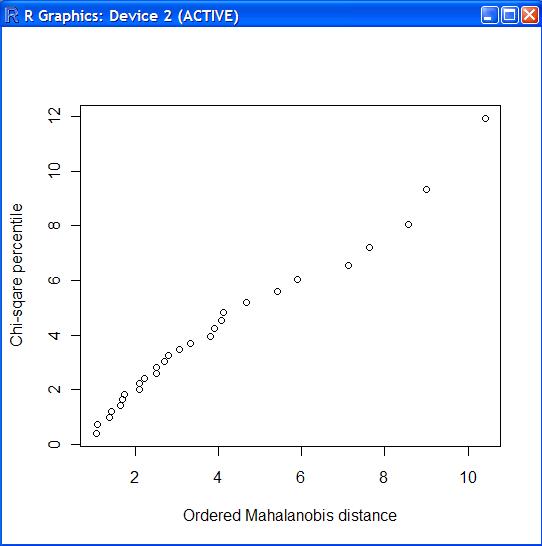
[edit]
5 베타그림 #
betaplot.f<-function(x)
{
n<-nrow(x)
p<-ncol(x)
alpha<-(p-2)/(2*p)
beta<-(n-p-3)/(2*(n-p-1))
mah<-sort((n/(n-1)^2)*mahalanobis(x,mean(x),var(x)))
start<-(1-alpha)/(n-alpha-beta+1)
step<-1/(n-alpha-beta+1)
arr<-seq(from=start,length=n,by=step)
beta.per<-qbeta(arr,alpha,beta)
plot(mah,beta.per,xlab="Ordered b_r",ylab="Beta percentile")
}
> source("betaplot.f")
> betaplot.f(cork.d)
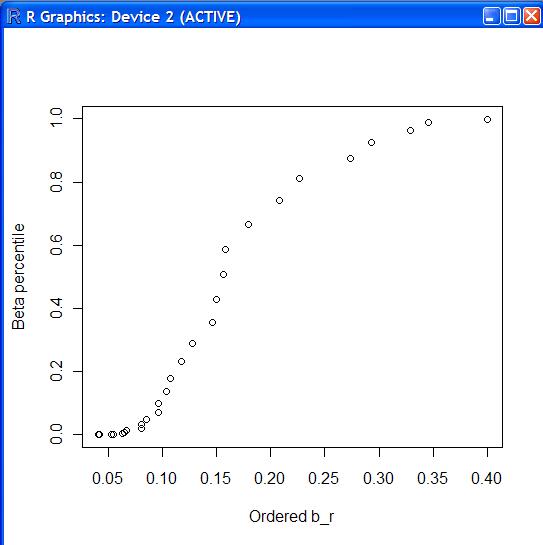
정규성을 가지고 있으나, 꼬리 부분이 약간 짧은 것으로 해석할 수 있다.
[edit]
6 Shapiro 검정 #
- 귀무가설: 정규분포를 따른다. (p-value > 0.05)
- 대립가설: 정규분포를 따르지 않는다. (p-value < 0.05)
> source("rftn.f")
> rad.d <-read.table("rad.d", header=T)
> shapiro.test(rad.d$open)
Shapiro-Wilk normality test
data: rad.d$open
W = 0.8292, p-value = 1.977e-05
p-value < 0.05 이므로 정규분포를 따르지 않는다.
[edit]
7 Box-Cox Transformation #
정규 분포에 가깝도록 변환하는 방법
mult.f<-function(lambda, x)
{
n<-nrow(x)
p<-ncol(x)
H<-rep(1,n)%*%t(rep(1,n))/n
Y<-matrix(0,n,p)
for(r in 1:n) {
for(i in 1:p) {
if( lambda[i] == 0 )
Y[r,i]<-log(x[r,i])
else
Y[r,i]<-(x[r,i]^lambda[i] - 1)/lambda[i]
}
}
Z<-matrix(0,n,p)
for(i in 1:p) {
a<-(prod(x[,i]))^((lambda[i]-1)/n)
Z[,i]<-Y[,i]/a
}
log(prod(eigen(t(Z)%*%(diag(n)-H)%*%Z)$values))
}
univ.f<-function(lambda, x)
{
n<-length(x)
H<-rep(1,n) %*% t(rep(1,n))/n
Y<-rep(0,n)
for(r in 1:n) {
if( lambda == 0 )
Y[r]<-log(x[r])
else
Y[r]<-(x[r]^lambda-1)/lambda
}
Y<-Y/(prod(x)^((lambda-1)/n))
t(Y)%*%(diag(n)-H)%*%Y
}
boxcox.f<-function(x)
{
x<-as.matrix(x)
p<-ncol(x)
sp<-rep(1,p)
for(i in 1:p) {
sp[i]<-nlminb(objective=univ.f,start=sp[i],x=x[,i])$par
}
lambda=nlminb(objective=mult.f,start=sp,x=x)$par
cat("Box-Cox parameters : ",lambda,"\n");
}
> source("boxcox.f")
> source("univ.f")
> source("mult.f")
> rad.d <-read.table("rad.d", header=T)
> chiplot.f(rad.d)
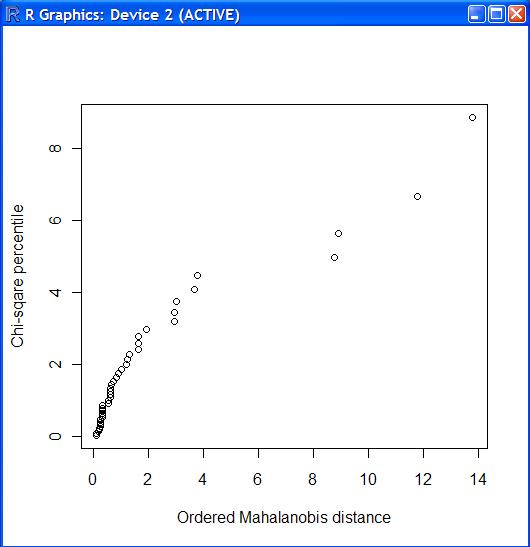
> boxcox.f(rad.d) Box-Cox parameters : 0.1607892 0.1511725
- lamda1 = 0.16
- lamda2 = 0.15
- closed = (closed ^ lamda1 - 1) / lamda1
- open = (open ^ lamda2 - 1) / lamda2
> boxcox_trans.d <- rad.d
> boxcox_trans.d$closed <- (rad.d$closed ^ 0.16 - 1) / 0.16
> boxcox_trans.d$open <- (rad.d$open ^ 0.15 - 1) / 0.15
> boxcox_trans.d
closed open
1 -1.6362440 -1.1015160
2 -1.9983371 -2.0210313
3 -1.4996718 -1.1015160
4 -1.9260564 -1.9470281
5 -2.3799621 -1.9470281
6 -1.7980629 -1.8161732
7 -2.0777107 -2.0210313
8 -2.3799621 -1.9470281
9 -2.0777107 -2.0210313
10 -1.9260564 -1.9470281
11 -2.1659062 -2.1928988
...
...
> chiplot.f(boxcox_trans.d)
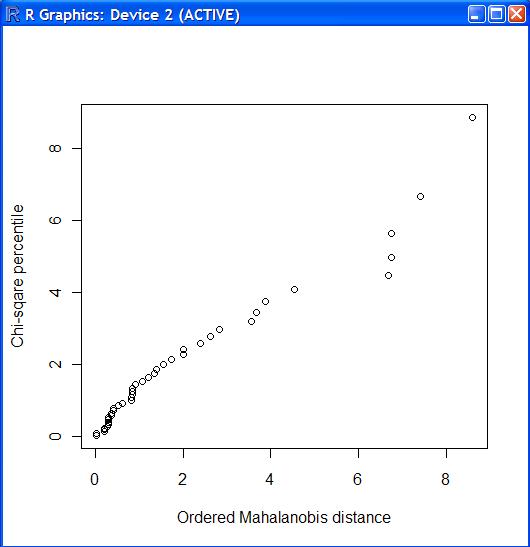
아니면..
install.packages("TeachingDemos")
library("TeachingDemos")
set.seed(12345)
x <- rnorm(150,1,1)
e <- rnorm(150,0,2)
y <- (.6 *x + 13 + e)^3
hist(y)
hist(bct(y, 0.39))
shapiro.test(bct(y, 0.39))
이렇게.. bct의 2번째 매개변수 lamda를 적절히 조절(0.1~0.9)해 가면서 정규분포로 만든다..
![[-] [-]](/moniwiki/imgs/plugin/arrup.png)
![[+] [+]](/moniwiki/imgs/plugin/arrdown.png)