Contents
- 1 shape
- 2 к≤єм≥РкЈЄл¶ђкЄ∞
- 3 histнХ®мИШмЧР boxplot мґФк∞АнХШкЄ∞
- 4 histнХ®мИШмЧР line мґФк∞АнХШкЄ∞
- 5 sigma level
- 6 лПДмИШлґДнПђнСЬ(нЮИмК§нЖ†кЈЄлЮ®)
- 7 мК§нКЬмХДмІАмК§ л∞©л≤Х
- 8 нСЬм§АнОЄм∞®л•Љ мЭімЪ©нХШлКФ л∞©л≤Х
- 9 5лЛ®к≥Д нПЙк∞А
- 10 кЄ∞нГА
- 11 RмЭД мЭімЪ©нХЬ нЮИмК§нЖ†кЈЄлЮ®
- 12 кЈЄл£єл≥Дл°Ь
- 13 2D нЮИмК§нЖ†кЈЄлЮ®
[edit]
2 к≤єм≥РкЈЄл¶ђкЄ∞ #
rgb()л°Ь rgb(red, green, blue, alpha ..) мГЙкєФ, нИђл™ЕлПДл•Љ м°∞м†ХнХЬлЛ§.
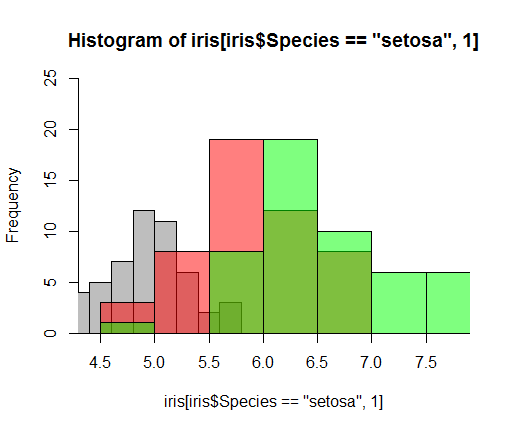
hist(iris[iris$Species =="setosa", 1], col="grey", xlim=range(iris$Sepal.Length), ylim=c(0,25)) hist(iris[iris$Species =="versicolor", 1], col=rgb(1, 0, 0, 0.5), add=TRUE) hist(iris[iris$Species =="virginica", 1], col=rgb(0, 1, 0, 0.5), add=TRUE)

[edit]
3 histнХ®мИШмЧР boxplot мґФк∞АнХШкЄ∞ #
hist(iris$Sepal.Length) sfsmisc::histBxp(iris$Sepal.Length)
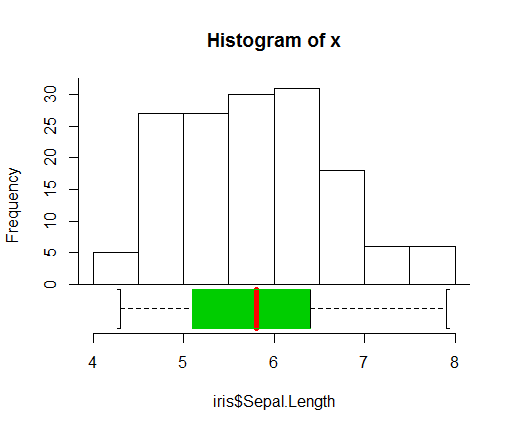
library(packHV) hist_boxplot(iris$Sepal.Length)
[edit]
4 histнХ®мИШмЧР line мґФк∞АнХШкЄ∞ #
л∞©л≤Х: https://cran.r-project.org/doc/contrib/Lemon-kickstart/kr_adlin.html
rescale<-function(x,newrange) {
if(nargs() > 1 && is.numeric(x) && is.numeric(newrange)) {
# if newrange has max first, reverse it
if(newrange[1] > newrange[2]) {
newmin<-newrange[2]
newrange[2]<-newrange[1]
newrange[1]<-newmin
}
xrange<-range(x)
if(xrange[1] == xrange[2]) stop("can't rescale a constant vector!")
mfac<-(newrange[2]-newrange[1])/(xrange[2]-xrange[1])
invisible(newrange[1]+(x-xrange[1])*mfac)
}
else {
cat("Usage: rescale(x,newrange)\n")
cat("\twhere x is a numeric object and newrange is the min and max of the new range\n")
}
}
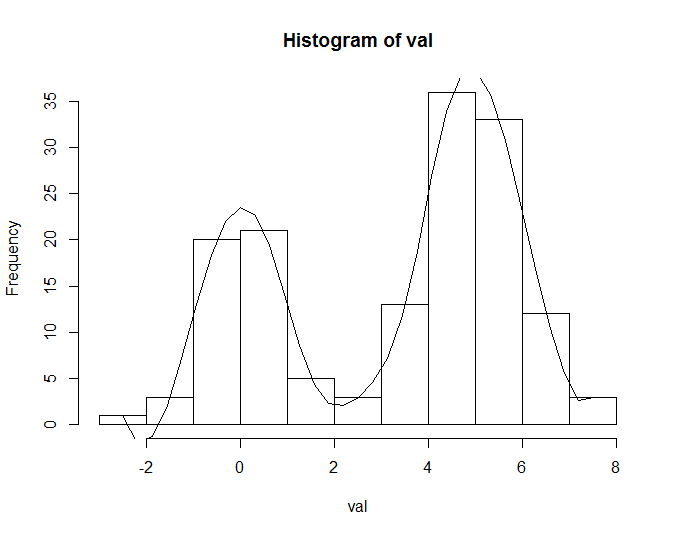
set.seed(1)
val1 <- rnorm(50)
set.seed(100)
val2 <- rnorm(100) + 5
val <- c(val1, val2)
h <- hist(val)
plot(h)
lines(rescale(spline(h$counts)$x, range(h$mids)), spline(h$counts)$y)
[edit]
6 лПДмИШлґДнПђнСЬ(нЮИмК§нЖ†кЈЄлЮ®) #
мЦілЦ§ лН∞мЭінД∞к∞А м†Дм≤і м§СмЧР м∞®мІАнХШлКФ мЬДмєШл•Љ мХМмХДлВікЄ∞ мЬДнХімДЬлКФ м†Дм≤і к≤љнЦ•мЭД нММмХЕнХШлКФ мЭЉмЭі лІ§мЪ∞ м§СмЪФнХШлЛ§. м†Дм≤і к≤љнЦ•мЭД нММмХЕнХШлКФлН∞лКФ лПДмИШлґДнПђнСЬк∞А лІ§мЪ∞ мЬ†мЪ©нХШлЛ§. лПДмИШлґДнПђнСЬлКФ лЛ§мЭМк≥Љ к∞ЩмЭА л∞©л≤ХмЬЉл°Ь лІМлУ§ мИШ мЮИлЛ§.
- лН∞мЭінД∞мЭШ мµЬлМА, мµЬмЖМк∞ТмЭД кµђнХЬлЛ§.
- мЮРл£МмЭШ нБђкЄ∞мЧР лФ∞лЭЉ м†БлЛєнХЬ к≥ДкЄЙмЭШ мИШл•Љ м†ХнХЬлЛ§.(мЭімГБмєШлКФ м†Ьк±∞нХЬлЛ§.(мЭімГБмєШ м†Ьк±∞ л∞©л≤Х))
- м§Сл≥µлРШмІА мХКк≤М к≥ДкЄЙмЭШ нБђкЄ∞л•Љ м†ХнХЬлЛ§.
- к∞Б к≥ДкЄЙмЧР мЖНнХШлКФ лПДмИШ(лН∞мЭінД∞ мИШ)л•Љ кµђнХЬлЛ§.
- к≥ДкЄЙмЭА мЧ∞мЖНмЬЉл°Ь нСЬмЛЬнХЬлЛ§.
- мГБлМАлПДмИШл•Љ кµђнХЬлЛ§. (мГБлМАлПДмИШ = нХілЛє к≥ДкЄЙмЭШ лПДмИШ / м†Дм≤і лПДмИШ)
[edit]
7 мК§нКЬмХДмІАмК§ л∞©л≤Х #
мК§нКЬмХДмІАмК§мЭШ л∞©л≤ХмЭА нЖµк≥ДнХЩ м±ЕмЭШ к±∞мЭШ м≤ШмЭМ лґАлґДмЧР лВШмШ§лКФ лВімЪ©мЭілЛ§. мК§нКЬмХДмІАмК§лКФ к≥ДкЄЙмЭШ мИШ[1]л•Љ к≤∞м†ХнХШлКФ л∞©л≤ХмЬЉл°Ь лЛ§мЭМк≥Љ к∞ЩмЭА к≥µмЛЭмЭД лІМлУ§мЧИлЛ§.
- к≥ДкЄЙмЭШ мИШ k = 1 + (log10N / log102) (N; мЮРл£МмЭШ мИШ) = 1 + (LOG10(N) / LOG10(2))
- к≥ДкЄЙмЭШ л≤ФмЬД R = (Maxк∞Т - Minк∞Т) / k
- лН∞мЭінД∞мЭШ міЭ к∞ЬмИШ, Maxк∞Т, Minк∞ТмЭД кµђнХЬлЛ§. мЭі лХМ Maxк∞Т, Minк∞ТмЭД кµђнХ† лХМлКФ мЭімГБмєШл•Љ м†Ьк±∞нХШлКФ к≤ГмЭі мҐЛлЛ§.
- мК§нКЬмХДмІАмК§мЭШ л∞©л≤ХмЭД мЭімЪ©нХШмЧђ к≥ДкЄЙмЭШ мИШ(k)л•Љ кµђнХЬлЛ§.
- мЬЧ лЛ®к≥ДмЧРмДЬ кµђнХімІД к≥ДкЄЙмЭШ мИШ kл•Љ мЭімЪФнХШмЧђ к∞ТмЭШ л≤ФмЬДл•Љ кµђнХЬлЛ§.
- кµђнХімІД л≤ФмЬДл°Ь лН∞мЭінД∞л•Љ кµђлґДнХЬлЛ§.
DECLARE
@k int
, @r bigint
, @avg bigint
, @sigma bigint
, @min bigint
, @max bigint
, @cnt int
, @min_real bigint
, @max_real bigint
--1 + (LOG10(N) / LOG10(2))
SELECT
@sigma = STDEV(Score)
, @avg = AVG(Score)
, @min_real = MIN(Score)
, @max_real = MAX(Score)
FROM #Score
-- мЭімГБмєШ м†Ьк±∞нЫД кµђк∞ДмЭД кµђнХЬлЛ§.: нПЙкЈ† - (1.5 * нСЬм§АнОЄм∞®) ~ нПЙкЈ† + (1.5 * нСЬм§АнОЄм∞®)
SELECT
@r = (MAX(Score) - MIN(Score)) / (1 + (LOG10(COUNT(*)) / LOG10(2)))
, @k = (1 + (LOG10(COUNT(*)) / LOG10(2)))
, @cnt = COUNT(*)
, @min = MIN(Score)
, @max = MAX(Score)
FROM #Score
WHERE Score > @avg - (3 * @sigma)
AND Score < @avg + (3 * @sigma)
;WITH Dumy(Seq)
AS
(
SELECT 1 Seq
UNION ALL
SELECT Seq + 1 FROM Dumy
WHERE Seq + 1 <= @k
), Grade
AS
(
SELECT
(@k - Seq ) + 1 Grade
, @min + ((Seq-1) * @r) BeginScore
, @min + (Seq * @r) EndScore
FROM Dumy
), RealGrade
AS
(
SELECT Grade, BeginScore, EndScore FROM Grade
UNION ALL
SELECT Grade + 1, @min_real, EndScore + 1
FROM Grade
WHERE Grade = (SELECT MAX(Grade) FROM Grade)
UNION ALL
SELECT Grade - 1, BeginScore + 1, @max_real
FROM Grade
WHERE Grade = (SELECT MIN(Grade) FROM Grade)
)
SELECT
B.Grade
, COUNT(*) AccountCnt
, SUM(NetAMT) NetAMT
FROM #Score A
INNER JOIN RealGrade B
ON A.Score BETWEEN B.BeginScore AND B.EndScore
GROUP BY
B.Grade
ORDER BY 1
[edit]
8 нСЬм§АнОЄм∞®л•Љ мЭімЪ©нХШлКФ л∞©л≤Х #
нСЬм§АнОЄм∞®л•Љ мЭімЪ©нХШл©і лЛ®мИЬнЮИ мЪ∞мИШ, л≥інЖµ, мЈ®мХљ мЭіл†Зк≤М 3к∞ЬмЭШ кЈЄл£ємЬЉл°Ь лВШлИМ мИШ мЮИлЛ§. мШИл•Љ лУ§мЦі, 50л™ЕмЭі м†ХмЫРмЭЄ нХЬ нХЩкЄЙмЧРмДЬ нХЩмГЭлУ§мЭШ нВ§мЧР лМАнХЬ нПЙкЈ†мєШк∞А 170CmмЭік≥†, нСЬм§АнОЄм∞®к∞А 7CmмШАмЭД лХМмЧР лЛ§мЭМк≥Љ к∞ЩмЭі лВШлЙ† мИШ мЮИлЛ§. (ѕГ[2]: нСЬм§АнОЄм∞®, ќЉ[3]: нПЙкЈ†)
- мЈ®мХљ: 163Cm лѓЄлІМ (ќЉ - ѕГ)
- л≥інЖµ: 163 ~ 177Cm (68.3%)
- мЪ∞мИШ: 177Cm міИк≥Љ (ќЉ + ѕГ)
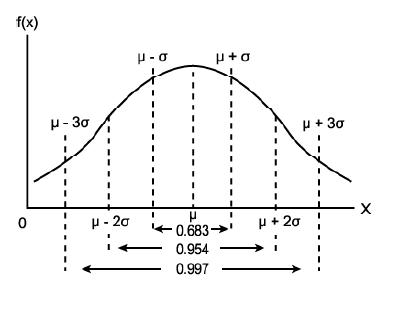 нСЬм§Ам†ХкЈЬлґДнПђ
нСЬм§Ам†ХкЈЬлґДнПђм∞Єк≥†л°Ь '6мЛЬкЈЄлІИ'мЭШ мЛЬкЈЄлІИлКФ мЬДмЭШ кЈЄл¶Љк≥Љ к∞ЩмЭА лЬїмЭД лВінПђнХШк≥† мЮИлЛ§. 6мЛЬкЈЄлІИлКФ (ќЉ - 6ѕГ) ~ (ќЉ + 6ѕГ)мЭШ кµђк∞ДмЭД лЬїмЭД лВШнГАлВЄлЛ§.
[edit]
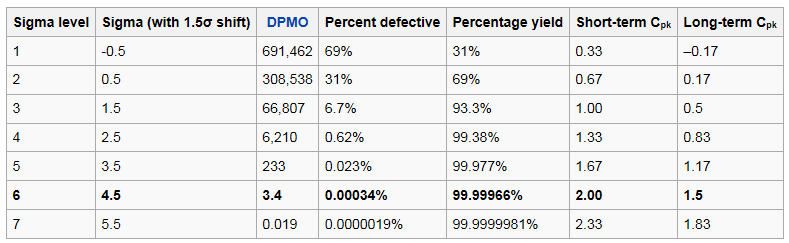
9 5лЛ®к≥Д нПЙк∞А #
мЬДмЭШ м†ХкЈЬлґДнПђмЧРмДЬ лЛ§мЭМк≥Љ к∞ЩмЭі 5к∞ЬмЭШ кµђк∞ДмЬЉл°Ь лВШлИМ мИШлПД мЮИлЛ§.
| кµђлґД | л≤ФмЬД | л≤ФмЬД(%) |
| E | (мµЬмЖМк∞Т) ~ (m - 1.5ѕГ) | 7% |
| D | (m - 1.5ѕГ) ~ (m - 0.5ѕГ) | 24% |
| C | (m - 0.5ѕГ) ~ (m + 0.5ѕГ) | 38% |
| B | (m + 0.5ѕГ) ~ (m + 1.5ѕГ) | 24% |
| A | (m + 1.5ѕГ) ~ (мµЬлМАк∞Т) | 7% |
[edit]
11 RмЭД мЭімЪ©нХЬ нЮИмК§нЖ†кЈЄлЮ® #
x <- rnorm(100)
xnm <- "м†ХкЈЬлґДнПђ"
hist(x, labels=TRUE, main = paste("Histogram of" , xnm), xlab = xnm)
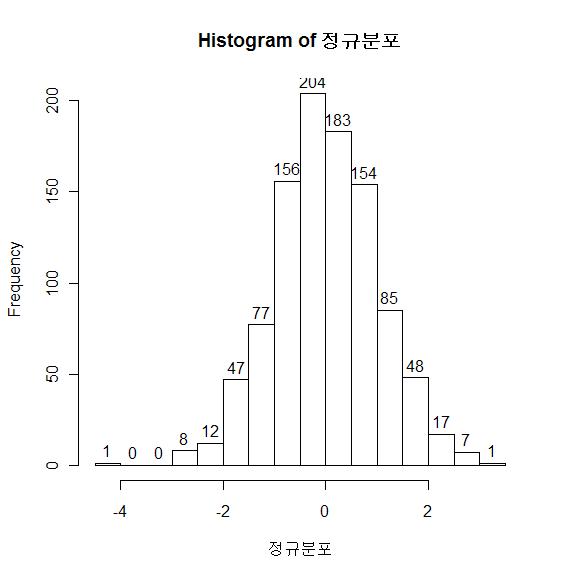
x <- rnorm(1000) hist(x, probability=T) lines(density(x))
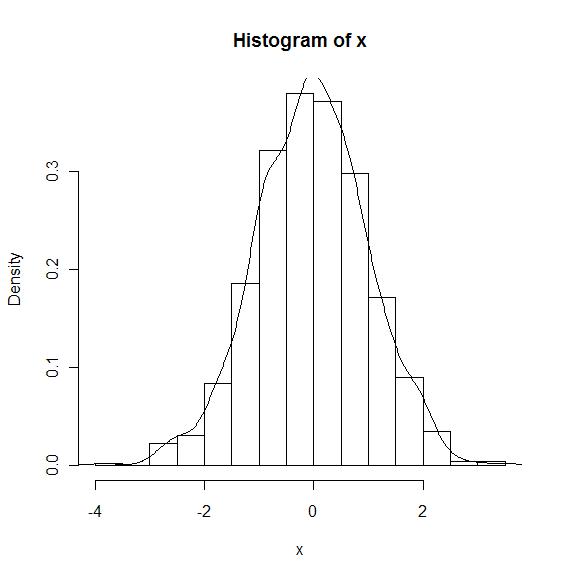
[edit]
12 кЈЄл£єл≥Дл°Ь #
install.packages("sm")
library("sm")
y <- c(1,2,3)
levels(x9$lf_group) <- c("group1", "group2", "group3")
sm.density.compare(x9$frd_cnt, x9$lf_group)
legend("topright", levels(x9$lf_group), fill=2+(0:nlevels(x9$lf_group)))
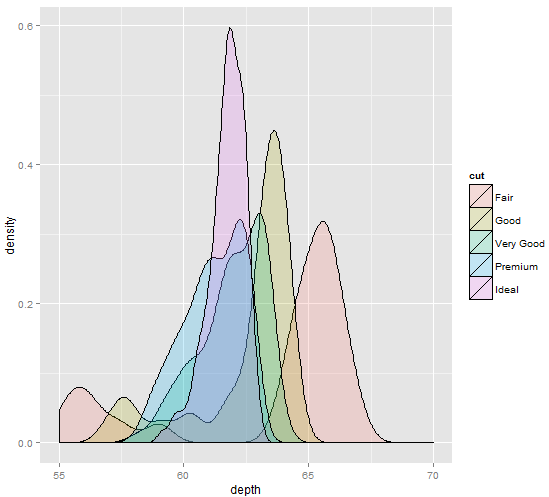
library("ggplot2")
diamonds_small <- diamonds[sample(nrow(diamonds), 1000), ]
ggplot(diamonds_small, aes(depth, fill = cut)) + geom_density(alpha = 0.2) + xlim(55, 70)