Contents

[-]
1 포아송 분포
2 예제


[edit]

1 포아송 분포 #

  • 단위시간이나 단위공간에서 어떤 사상이 발생할 확률을 구하기 위해 사용
  • 예
    • 단위시간 내에 찾아오는 고객의 수
    • 단위면적당 직물의 결함수
    • 어떤 지역의 하루 교통사고 건수
  • 전제조건
    • 단위시간이나 단위공간에서 사상이 발생할 확률은 동일
    • 두 개 이상의 사상이 극히 작은 공간에서 발생할 확률은 무시할 정도로 작음
    • 단위시간이나 단위공간 내 사상의 발생은 서로 독립이다.
  • 가장 중요한 모수(parameter)는 '단위시간당 평균 발생률 λ(lambda)'
  • 어떤 주어진 간격 사이에 어떤 사건이 일어날 기대값이 λ라 하면, 사건이 k회 일어날 확률은 다음과 같이 정의
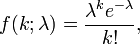
    poisson01.png
  • e: 상수로 자연로그의 밑이 되는 수(e = 2.71828...)
  • k: 는 발생한 사건의 수.
  • λ: 평균 발생횟수(양의 실수로 어떤 주어진 간격안에 일어나는 사건의 기대치)
  • 엑셀함수: POISSON(k,λ,True or False)
  • 일반적으로 λ = np <5 이면 포아송 분포와 이항분포는 거의 같은 확률을 같는다.
    • n = 시행횟수
    • p = 성공확률

    • poisson_dist.jpg
    [edit]

    2 예제 #

    어떤 이발소에 1시간에 평균 3명의 손님이 찾아온다. 다음을 구하라
    • 1시간에 4명의 손님이 찾아올 확률
      • 0.168031356
      • =POISSON(4,3,FALSE)
    • 1시간에 4명 이하의 손님이 찾아올 확률
      • 0.815263245
      • =POISSON(4,3,TRUE)
    • 1시간에 4명 이상의 손님이 찾아올 확률
      • 0.352768111
      • 다음의 합
        • =POISSON(4,3,FALSE)
        • =POISSON(5,3,FALSE)
        • =POISSON(6,3,FALSE)
        • ... (0값이 나올때까지 계속 k값을 증가시킨다)
        • =POISSON(23,3,FALSE)
      • 또는 = 1 - POISSON(3,3,True)

    어느 도시의 하루 교통사고 사망자수는 λ = 1.5 포아송 분포를 따른다. 포아송 분포표를 이용하여'

    • 포아송 분포표
    • 하루 동안 3명이 사망할 확률: 0.125510715
    • 하루 동안 2명 이하가 사망할 확률: 0.808846831
    • 하루 동안 5명 이상이 사망할 확률: 0.018575936
      poisson02.jpg