[edit]
1 в│ђВѕўВЮў ьўЋьЃю #
- ВъљвБї(data)въђ, Ж┤ђВИАВ╣ў(observation)вЊцВЮў ВДЉьЋЕ.
- в│ђВѕў(variable)въђ, ВІюЖ░ёВЌљ вћ░вЮ╝ в│ђьЋўвіћ Вќ┤вќц ьі╣Вё▒ вўљвіћ ьі╣ВаЋ ВІюВаљВЌљВёю вІцвЦИ ВѓгвъїВЮ┤вѓў вг╝В▓┤Ж░ёВЌљ в│ђьЋўвіћ Вќ┤вќц ьі╣Вё▒ВЮё вДљьЋювІц. (= в│ђвЪЅ)
- ВДѕВаЂ в│ђВѕўВЎђ ВќЉВаЂ в│ђВѕў
- ВДѕВаЂ в│ђВѕў
- ьі╣Вё▒ВЃЂ ВѕўВ╣ўвАю вѓўьЃђвѓ┤Ж▒░вѓў вўљвіћ ВѕўВ╣ўвАю вѓўьЃђвѓ╝ Вѕў ВЌєвіћ в│ђВѕў
- Вё▒в│ё, ВбЁЖхљ, ВДЂВЌЁ вЊ▒
- ВДѕВаЂ в│ђВѕўВЌљ вїђьЋю ВИАВаЋВъљвБївЦ╝ ВДѕВаЂ ВъљвБї, ВаЋВё▒ВаЂ ВъљвБї вўљвіћ в▓ћВБ╝ВаЂ ВъљвБї(categorical data)вЮ╝Ж│а ьЋе
- вфЁвфЕ, ВёюВЌ┤ ВъљвБїЖ░ђ ьЈгьЋевље.
- ВќИВаювѓў ВЮ┤Вѓ░ВаЂ ВъљвБї
- ьі╣Вё▒ВЃЂ ВѕўВ╣ўвАю вѓўьЃђвѓ┤Ж▒░вѓў вўљвіћ ВѕўВ╣ўвАю вѓўьЃђвѓ╝ Вѕў ВЌєвіћ в│ђВѕў
- ВќЉВаЂ в│ђВѕў
- ьі╣Вё▒ВЃЂ ВѕўВ╣ўвАю вѓўьЃђвѓ╝ Вѕў Въѕвіћ в│ђВѕў
- ВўѕЖИѕВъћВЋА, ВъљвЁђВѕў, В▓┤ВцЉ вЊ▒
- ВќЉВаЂ в│ђВѕўВЌљ вїђьЋю ВИАВаЋВъљвБївЦ╝ ВќЉВаЂ ВъљвБї вўљвіћ ВаЋвЪЅВаЂ ВъљвБївЮ╝Ж│а ьЋе
- ВќЉВаЂ в│ђВѕўВЮў вХёвЦў
- ВЌ░ВєЇВаЂ в│ђВѕў(continuous variable)
- ВЮ┤Вѓ░ВаЂ в│ђВѕў(discrete variable) -> Ж░њ ВѓгВЮ┤ВЌљ GapВЮё Ж░ќЖ▓ї вље
- ВЌ░ВєЇВаЂ в│ђВѕў(continuous variable)
- ЖхгЖ░ёВъљвБї, в╣ёВюеВъљвБїЖ░ђ ьЈгьЋевље
- ьі╣Вё▒ВЃЂ ВѕўВ╣ўвАю вѓўьЃђвѓ╝ Вѕў Въѕвіћ в│ђВѕў
- ВДѕВаЂ в│ђВѕў
- вІев│ђВѕўВЎђ вІцв│ђВѕў
- Ж┤ђВИА вїђВЃЂВЮ┤ вљўвіћ Ж░Ђ ЖИ░в│ИвІеВюёЖ░ђ ьЋўвѓўВЮў в│ђВѕўвЦ╝ Ж░ќвіћ ВъљвБї. в│ђВѕўЖ░ђ ьЋўвѓўВЮ┤ЖИ░ вЋївгИВЌљ ВъљвБїВЮў вїђьЉюВ╣ў, ЖИ░в│ИвІеВюёвЊцВЮў вЈЎВДѕВё▒, ВЮ┤ВЃЂВ╣ў(oulier)ВЮў ВА┤ВъгВЌгвХђ вЊ▒ВЌљ Ж┤ђьЋю ьі╣Вё▒ВЮё ВџћВЋйьЋўвіћ ьєхЖ│ёвХёВёЮ в░Ев▓ЋВЮ┤ ВѓгВџЕвље.
- Ж┤ђВИА вїђВЃЂВЮ┤ вљўвіћ Ж░Ђ ЖИ░в│ИвІеВюёЖ░ђ ВЌгвЪгЖ░юВЮў в│ђВѕўвЦ╝ Ж░ќвіћ ВъљвБї. в│ђВѕўЖ░ђ вЉљ Ж░ю ВЮ┤ВЃЂВЮ┤в»ђвАю вІев│ђВѕў ВъљвБїВЌљВёю Вќ╗віћ ьі╣Вё▒ ВЮ┤ВЎИВЌљ в│ђВѕўЖ░ёВЮў Ж┤ђЖ│ё, в│ђВѕўЖ░ёВЮў в░ђВаЉВё▒, ьЋю в│ђВѕўвАювХђьё░ вІцвЦИ в│ђВѕўВЮў Ж░њ ВўѕВИА вЊ▒ВЮў в░Юьъѕвіћ ьєхЖ│ёвХёВёЮв░Ев▓ЋВЮ┤ ВѓгВџЕвље.
- Ж┤ђВИА вїђВЃЂВЮ┤ вљўвіћ Ж░Ђ ЖИ░в│ИвІеВюёЖ░ђ ьЋўвѓўВЮў в│ђВѕўвЦ╝ Ж░ќвіћ ВъљвБї. в│ђВѕўЖ░ђ ьЋўвѓўВЮ┤ЖИ░ вЋївгИВЌљ ВъљвБїВЮў вїђьЉюВ╣ў, ЖИ░в│ИвІеВюёвЊцВЮў вЈЎВДѕВё▒, ВЮ┤ВЃЂВ╣ў(oulier)ВЮў ВА┤ВъгВЌгвХђ вЊ▒ВЌљ Ж┤ђьЋю ьі╣Вё▒ВЮё ВџћВЋйьЋўвіћ ьєхЖ│ёвХёВёЮ в░Ев▓ЋВЮ┤ ВѓгВџЕвље.
| ВбЁВЌЁВЏљ | ВЮИВбЁ | Вё▒ | ВДЂВюё | Жи╝вг┤ВЌ░Вѕў | ВЌ░в┤Ѕ |
| ьЎЇЖИИвЈЎ | ьЎЕ | вѓе | Ж│╝ВъЦ | 5 | 6 |
| ВъЦЖИИВѓ░ | ьЎЕ | вѓе | вїђвдг | 3 | 3 |
| Ж░юВєївгИ | ьЎЕ | вѓе | вХђВъЦ | 7 | 5 |
| ВіцьЃѕвд░ | в░▒ | вѓе | вїђвдг | 2 | 1 |
| вДѕвЈѕвѓў | в░▒ | ВЌг | Ж│╝ВъЦ | 6 | 3 |
- ЖИ░в│ИвІеВюёвіћ? ьЎЇЖИИвЈЎ, ВъЦЖИИВѓ░, Ж░юВєївгИ, ВіцьЃѕвд░, вДѕвЈѕвѓў
- в│ђВѕўвіћ? ВбЁВЌЁВЏљ, ВЮИВбЁ, Вё▒, ВДЂВюё, Жи╝вг┤ВЌ░Вѕў, ВЌ░в┤Ѕ
- ВДѕВаЂ? ВќЉВаЂ?
- ВДѕВаЂв│ђВѕў: ВЮИВбЁ, Вё▒, ВДЂВюё
- ВќЉВаЂв│ђВѕў: Жи╝вг┤ВЌ░Вѕў, ВЌ░в┤Ѕ (вфевЉљ ВЌ░ВєЇВаЂ)
- ВДѕВаЂв│ђВѕў: ВЮИВбЁ, Вё▒, ВДЂВюё
- ВДЂВюёВЮў вфеВДЉвІе? вХђВъЦ, Ж│╝ВъЦ, вїђвдг
- ВъљвБїВЮў Вѕўвіћ? 25
- вІцв│ђвЪЅ ВъљвБї
[edit]
2 ВИАВаЋВ▓ЎвЈёВЮў ьўЋьЃю #
4Ж░ђВДђ ьўЋьЃю
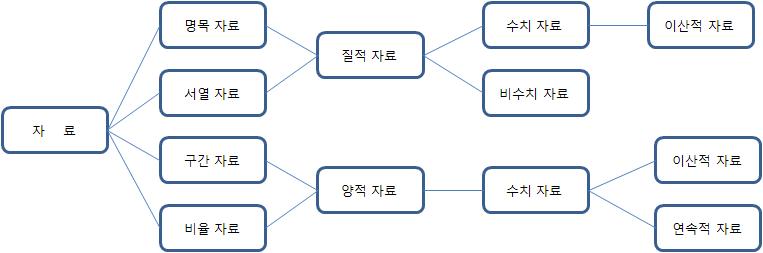
- вфЁвфЕВ▓ЎвЈё(nominal scale)
- Ж░њВЮђ в▓ћВБ╝(category) вўљвіћ ваѕВЮ┤вИћ(label)
- Вё▒в│ё, ВЮ┤вЕћВЮИВЮИВдЮВЌгвХђ, ВДЂВюё вЊ▒
- '=' вўљвіћ '<>'вДї Ж░ђВДђЖ│а в╣ёЖхљ Ж░ђвіЦ
- Ж░њВЮђ в▓ћВБ╝(category) вўљвіћ ваѕВЮ┤вИћ(label)
- ВёюВЌ┤В▓ЎвЈё(ordinal scale)
- Ж░њВЮђ ВИАВаЋ вїђВЃЂЖ░ёВЮў вєњ/вѓ«, ьЂ╝/ВъЉВЮї, Вёа/ьЏё вЊ▒ВЮў ВёюВЌ┤ ВѕюВёювЦ╝ Ж░ђВДљ
- ьЋЎВаљ, вІеВюё(KB, MB, TB, PB..) вЊ▒
- '=', '<>', '>=', '<=' ВЌ░Вѓ░ Ж░ђвіЦ
- Ж░њВЮђ ВИАВаЋ вїђВЃЂЖ░ёВЮў вєњ/вѓ«, ьЂ╝/ВъЉВЮї, Вёа/ьЏё вЊ▒ВЮў ВёюВЌ┤ ВѕюВёювЦ╝ Ж░ђВДљ
- ЖхгЖ░ёВ▓ЎвЈё(interval scale)
- Ж░њвЊцВЮ┤ ВЮ╝ВаЋьЋю В░еВЮ┤вДїьЂ╝ ВЮ╝ВаЋьЋю ьЂгЖИ░вЦ╝ Ж░ђВДёвІц.(вфЁвфЕ, ВёюВЌ┤ ВъљвБїВЮў ьі╣Вё▒ВЮё Ж░ђВДљ)
- ВўевЈё, ВДђвіЦВДђВѕў, ьЋЎвЁё вЊ▒
- "ВБ╝ВЮў" ВъљвБївЊцЖ░ёВЮў В░еВЮ┤(Ж░ёЖ▓Е)Ж░ђ ВЮўв»И ВъѕВЮё в┐љВЮ┤ВДђ В░еВЮ┤ВЮў в╣ёВюеВЮђ ВЮўв»ИЖ░ђ ВЌєвІц. (ВўевЈёЖ░ђ ВёюВџИ 15вЈё, вХђВѓ░ 30вЈё вЮ╝Ж│а ьЋ┤вЈё вХђВѓ░ВЮ┤ 2в░░вЇћ вЇЦвІцЖ│а ьЋа Вѕў ВЌєвІц) -> ВЃЂвїђВаЂВЮИ ВюёВ╣ўвДї вѓўьЃђвѓ╝ в┐љ
- '=', '<>', '>=', '<=', '+', '-' ВЌ░Вѓ░ Ж░ђвіЦ
- Ж░њвЊцВЮ┤ ВЮ╝ВаЋьЋю В░еВЮ┤вДїьЂ╝ ВЮ╝ВаЋьЋю ьЂгЖИ░вЦ╝ Ж░ђВДёвІц.(вфЁвфЕ, ВёюВЌ┤ ВъљвБїВЮў ьі╣Вё▒ВЮё Ж░ђВДљ)
- в╣ёВюеВ▓ЎвЈё(ratio scale)
- вфЁвфЕ, ВёюВЌ┤, ЖхгЖ░ё ВъљвБїВЮў вфевЊа ьі╣Вё▒ВЮё Ж░ђВДѕ в┐љвДї ВЋёвІѕвЮ╝ ВаѕвїђВаЂ ВюёВ╣ўвЦ╝ вѓўьЃђвѓ┤віћ ВЏљВаљ(0)ВЮё Ж░ђВДђЖИ░ вЋївгИВЌљ вЉљ ВИАВаЋВ╣ў ВѓгВЮ┤ВЮў в╣ёВюеВЮё Ж│ёВѓ░ьЋа Вѕў ВъѕвІц.
- AВЮў ВЏћЖИЅВЮ┤ 100ВЏљВЮ┤Ж│а, BВЮў ВЏћЖИЅВЮ┤ 200ВЏљВЮ┤вЕ┤ BВЮў ВЏћЖИЅВЮ┤ Aв│┤вІц 2в░░вЇћ вДјвІцЖ│а ВЮ┤ВЋ╝ЖИ░ ьЋа Вѕў ВъѕвІц.
- * '=', '<>', '>=', '<=', '+', '-', '/', '*' ВЌ░Вѓ░ Ж░ђвіЦ
- вфЁвфЕ, ВёюВЌ┤, ЖхгЖ░ё ВъљвБїВЮў вфевЊа ьі╣Вё▒ВЮё Ж░ђВДѕ в┐љвДї ВЋёвІѕвЮ╝ ВаѕвїђВаЂ ВюёВ╣ўвЦ╝ вѓўьЃђвѓ┤віћ ВЏљВаљ(0)ВЮё Ж░ђВДђЖИ░ вЋївгИВЌљ вЉљ ВИАВаЋВ╣ў ВѓгВЮ┤ВЮў в╣ёВюеВЮё Ж│ёВѓ░ьЋа Вѕў ВъѕвІц.

ВІюЖ│ёВЌ┤ВъљвБїВЎђ ьџАвІевЕ┤ВъљвБї
- ВІюЖ│ёВЌ┤ВъљвБї(time series data), ВІюЖ░ёВЮў ВѕюВёювїђвАю ЖИ░вАЮ
- ьџАвІевЕ┤ВъљвБї(cross sectional data), ьі╣ВаЋ ВІюВаљВЌљ ВИАВаЋьЋўВЌг ЖИ░вАЮ
[edit]
3 ьєхЖ│ёьЉюВЎђ ЖиИвъўьћё #
вЈёВѕўвХёьЈгьЉю
- ВъљвБївЦ╝ ьЋю в│ђВѕўЖ░ђ Ж░ђВДѕ Вѕў Въѕвіћ Ж░њвЊцВЮў Ж│ёЖИЅ вўљвіћ в▓ћВБ╝вАю вѓўвѕёЖ│а Ж░Ђ Ж│ёЖИЅВЌљ ВєЇьЋўвіћ ВИАВаЋВ╣ўВЮў вЈёВѕўвЦ╝ вѓўьЃђвѓ┤віћ ьєхЖ│ёьЉю
- вЈёВѕў(freqeuncy), Ж░Ђ Ж│ёЖИЅВЌљ ьЋ┤вІ╣вљўвіћ Ж░њВЮў Ж░юВѕў
- ВЃЂвїђвЈёВѕў(relative freqeuncy), Ж░Ђ Ж│ёЖИЅВЌљ ВєЇьЋю вЈёВѕўЖ░ђ В┤ЮвЈёВѕўВЌљВёю В░еВДђьЋўвіћ в╣ёВюе
| ьЋЎвЁё | вЈёВѕў | ВЃЂвїђвЈёВѕў |
| 1ьЋЎвЁё | 1 | 0.1 |
| 2ьЋЎвЁё | 4 | 0.4 |
| 3ьЋЎвЁё | 3 | 0.3 |
| 4ьЋЎвЁё | 2 | 0.2 |
| В┤ЮвЈёВѕў | 10 | 1.0 |
[edit]
4 вЈёВѕўвХёьЈгьЉю(ьъѕВіцьєаЖиИвъе) #
Вќ┤вќц вЇ░ВЮ┤ьё░Ж░ђ ВаёВ▓┤ ВцЉВЌљ В░еВДђьЋўвіћ ВюёВ╣ўвЦ╝ ВЋїВЋёвѓ┤ЖИ░ ВюёьЋ┤Вёювіћ ВаёВ▓┤ Ж▓йьќЦВЮё ьїїВЋЁьЋўвіћ ВЮ╝ВЮ┤ вДцВџ░ ВцЉВџћьЋўвІц. ВаёВ▓┤ Ж▓йьќЦВЮё ьїїВЋЁьЋўвіћвЇ░віћ вЈёВѕўвХёьЈгьЉюЖ░ђ вДцВџ░ ВюаВџЕьЋўвІц. вЈёВѕўвХёьЈгьЉювіћ вІцВЮїЖ│╝ Ж░ЎВЮђ в░Ев▓ЋВю╝вАю вДївЊц Вѕў ВъѕвІц.
- вЇ░ВЮ┤ьё░ВЮў Вхювїђ, ВхюВєїЖ░њВЮё ЖхгьЋювІц.
- ВъљвБїВЮў ьЂгЖИ░ВЌљ вћ░вЮ╝ ВаЂвІ╣ьЋю Ж│ёЖИЅВЮў ВѕўвЦ╝ ВаЋьЋювІц.(ВЮ┤ВЃЂВ╣ўвіћ ВаюЖ▒░ьЋювІц.(ВЮ┤ВЃЂВ╣ў ВаюЖ▒░ в░Ев▓Ћ))
- ВцЉв│хвљўВДђ ВЋіЖ▓ї Ж│ёЖИЅВЮў ьЂгЖИ░вЦ╝ ВаЋьЋювІц.
- Ж░Ђ Ж│ёЖИЅВЌљ ВєЇьЋўвіћ вЈёВѕў(вЇ░ВЮ┤ьё░ Вѕў)вЦ╝ ЖхгьЋювІц.
- Ж│ёЖИЅВЮђ ВЌ░ВєЇВю╝вАю ьЉюВІюьЋювІц.
- ВЃЂвїђвЈёВѕўвЦ╝ ЖхгьЋювІц. (ВЃЂвїђвЈёВѕў = ьЋ┤вІ╣ Ж│ёЖИЅВЮў вЈёВѕў / ВаёВ▓┤ вЈёВѕў)
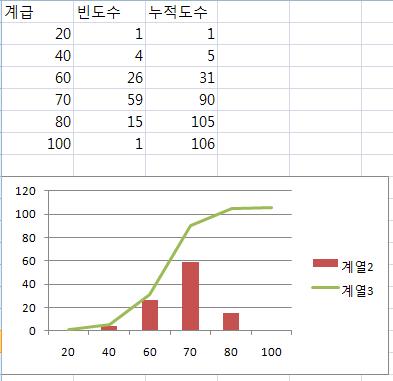
ВЌЉВЁђ2007ВЌљВёю вДЅвїђ ЖиИвъўьћёВЎђ Ж║йВЮђВёа ЖиИвъўьћёвЦ╝ вЈЎВІюВЌљ ьЉюьўёьЋўЖ│аВъљ ьЋювІцвЕ┤, Вџ░Вёа 2Ж░юВЮў Ж│ёВЌ┤ВЮё вфевЉљ вДЅвїђ ЖиИвъўьћёвАю ьЉюВІюьЋю ьЏё, вДѕВџ░Віц ВўцвЦИ ьЂ┤вдГьЋўВЌг вІцВЮї ЖиИвд╝Ж│╝ Ж░ЎВЮ┤ [Ж│ёВЌ┤ В░еьіИ ВбЁвЦў в│ђЖ▓й] ВЮё ьЂ┤вдГьЋўВЌг Ж║йВЮђВёа ЖиИвъўьћёвАю в│ђЖ▓йьЋювІц.
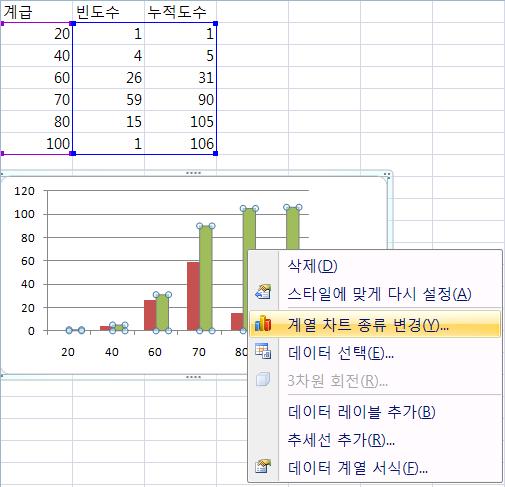
вІцВЮїВЮў в│ђЖ▓йвљю ЖиИвд╝ВЮ┤вІц.

[edit]
5 ВіцьіюВЋёВДђВіц в░Ев▓Ћ #
ВіцьіюВЋёВДђВіцВЮў в░Ев▓ЋВЮђ ьєхЖ│ёьЋЎ В▒ЁВЮў Ж▒░ВЮў В▓ўВЮї вХђвХёВЌљ вѓўВўцвіћ вѓ┤ВџЕВЮ┤вІц. ВіцьіюВЋёВДђВіцвіћ Ж│ёЖИЅВЮў Вѕў[1]вЦ╝ Ж▓░ВаЋьЋўвіћ в░Ев▓ЋВю╝вАю вІцВЮїЖ│╝ Ж░ЎВЮђ Ж│хВІЮВЮё вДївЊцВЌѕвІц. ьъѕВіцьєаЖиИвъеВЮё вДївЊцвЋї ВюаВџЕьЋўвІц.
- Ж│ёЖИЅВЮў Вѕў k = 1 + (log10N / log102) (N; ВъљвБїВЮў Вѕў) = 1 + (LOG10(N) / LOG10(2))
- Ж│ёЖИЅВЮў в▓ћВюё R = (MaxЖ░њ - MinЖ░њ) / k
- вЇ░ВЮ┤ьё░ВЮў В┤Ю Ж░юВѕў, MaxЖ░њ, MinЖ░њВЮё ЖхгьЋювІц. ВЮ┤ вЋї MaxЖ░њ, MinЖ░њВЮё ЖхгьЋа вЋївіћ ВЮ┤ВЃЂВ╣ўвЦ╝ ВаюЖ▒░ьЋўвіћ Ж▓ЃВЮ┤ ВбІвІц.
- ВіцьіюВЋёВДђВіцВЮў в░Ев▓ЋВЮё ВЮ┤ВџЕьЋўВЌг Ж│ёЖИЅВЮў Вѕў(k)вЦ╝ ЖхгьЋювІц.
- ВюЌ вІеЖ│ёВЌљВёю ЖхгьЋ┤ВДё Ж│ёЖИЅВЮў Вѕў kвЦ╝ ВЮ┤ВџЕьЋўВЌг Ж░њВЮў в▓ћВюёвЦ╝ ЖхгьЋювІц.
- ЖхгьЋ┤ВДё в▓ћВюёвАю вЇ░ВЮ┤ьё░вЦ╝ ЖхгвХёьЋювІц.
№╗┐
![[http]](/moniwiki/imgs/http.png)